transsetr.blogg.se - Surface area of a rectangular prism formula

#SURFACE AREA OF A RECTANGULAR PRISM FORMULA HOW TO#

The basic properties of a square prism are as follows: Here, a = the length of the side of the prism and h = the height of the prism What are the Properties of a Square Prism?

Surface Area of a square prism = 2a 2 + 4ah.

There are two basic formulas related to a square prism:

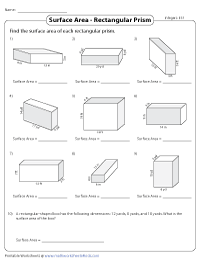
Therefore, all cubes can be square prisms, but all square prisms cannot be cubes. A cube is a three-dimensional solid figure with all its faces as squares. A square prism is a three-dimensional solid figure with six faces in which the two opposite faces are squares while the other four are rectangular. No, all square prisms are not the same as cubes. The base is in the shape of square, so A(base) = l².FAQs on Square Prism Is a Square Prism the Same as a Cube? Explain.

A = A(base) + A(lateral) = A(base) + 4 * A(lateral face).

A = l * √(l² + 4 * h²) + l² where l is a base side and h is a height of a pyramid.

The formula for surface area of a pyramid is: That’s the option which we used as a pyramid in this surface area calculator. Regular means that it has a regular polygon base and is a right pyramid (apex directly above the centroid of its base) and square – that it has this shape as a base. When you hear a pyramid, it’s usually assumed to be a regular square pyramid.

A = π * r * √(r² + h²) + π * r² given r and h.Ī pyramid is a 3D solid with a polygonal base and triangular lateral faces.

A = A(lateral) + A(base) = π * r * s + π * r² given r and s or.

Finally, add the areas of the base and the lateral part to find the final formula for surface area of a cone:.

Thus, the lateral surface area formula looks as follows:

r² + h²= s² so taking the square root we got s = √(r² + h²).

Usually we don’t have the s value given but h, which is the height of the cone. But that’s not a problem at all! We can easily transform the formula using Pythagorean theorem:.

(sector area) / (large circle area) = (arc length) / (large circle circumference) so.

The formula can be obtained from proportion: ratio of the areas of the shapes is the same as ratio of the arc length to the circumference:

The area of a sector – which is our lateral surface of a cone – is given by the formula:.

$surface area of a rectangular prism formula$

For the circle with radius s, the circumference is equal to 2 * π * s. The arc length of the sector is equal to 2 * π * r.Roll the lateral surface out flat. It’s a circular sector, which is the part of a circle with radius s ( s is the slant height of the cone).Let’s have a look at this step by step derivation: The base is again the area of a circle A(base) = π * r², but the lateral surface area origins may be not so obvious: A = A(lateral) + A(base), as we have only one base, in contrast to a cylinder.The surface area of a cone may also be split into two parts:

#SURFACE AREA OF A RECTANGULAR PRISM FORMULA HOW TO#

Surface area of a pyramid: A = l * √(l² + 4 * h²) + l², where l is a side length of the square base and h is a height of a pyramid.īut where do those formulas come from? How to find the surface area of the basic 3D shapes? Keep reading and you’ll find out!.Surface area of a triangular prism: A = 0.5 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) + h * (a + b + c), where a, b and c are the lengths of three sides of the triangular prism base and h is a height (length) of the prism.Surface area of a rectangular prism (box): A = 2(ab + bc + ac), where a, b and c are the lengths of three sides of the cuboid.Surface area of a cone: A = πr² + πr√(r² + h²), where r is the radius and h is the height of the cone.Surface area of a cylinder: A = 2πr² + 2πrh, where r is the radius and h is the height of the cylinder.Surface area of a cube: A = 6a², where a is the side length.Surface area of a sphere: A = 4πr², where r stands for the radius of the sphere.

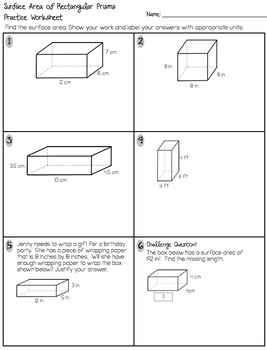
The formula depends on the type of the solid. Our surface area calculator can find the surface area of seven different solids.